Calculating the likelihood for an ultrametric tree (example)

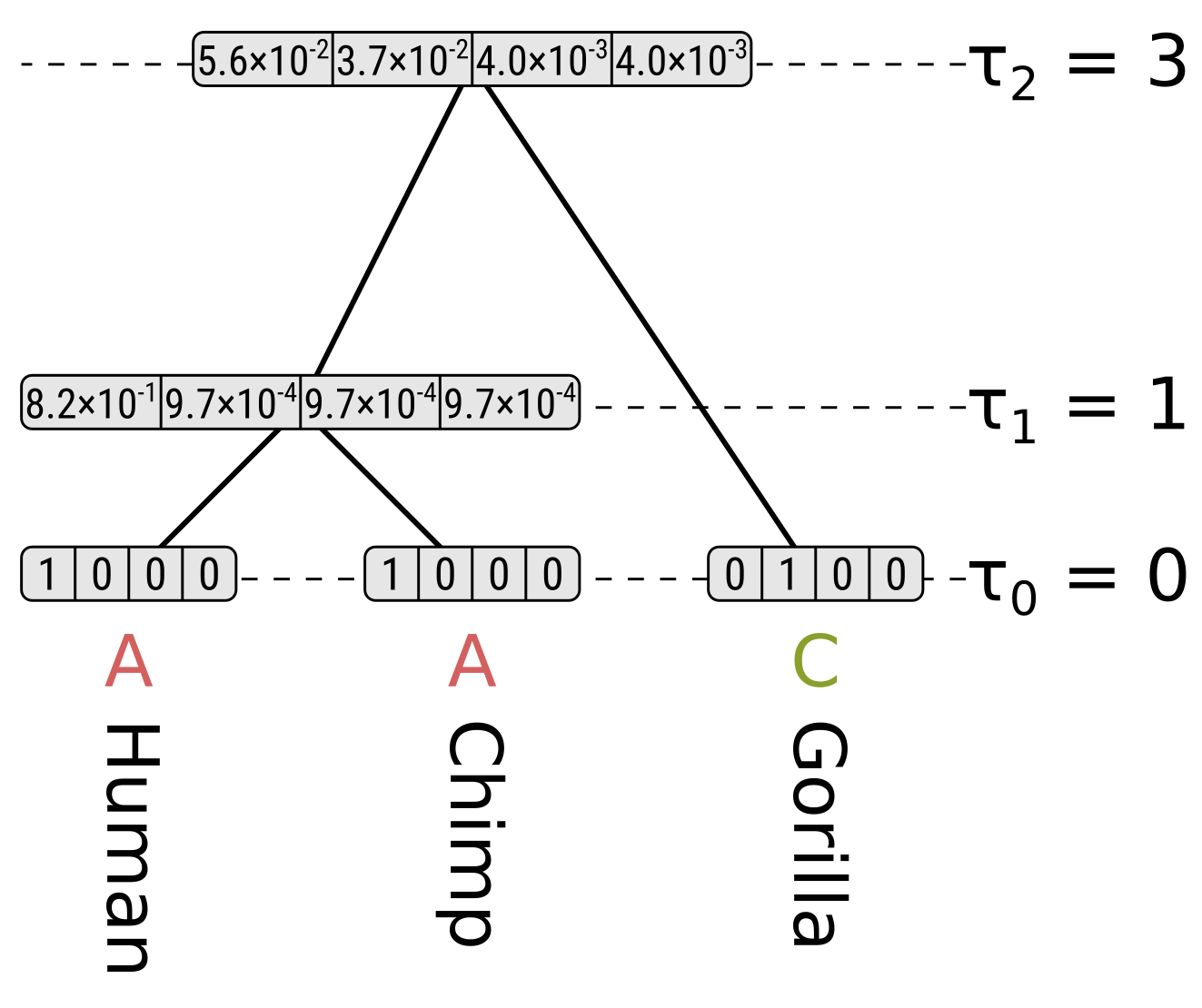
In this example we will calculate the likelihood \(P(D|T,h)\) where \(D\) is a single site, \(T\) is a rooted tree topology, and \(h\) is the node heights for the tree topology. Since we are using node heights instead of branch lengths, and if we make the node heights at the tips all zeros, the tree is necessarily ultrametric. The site pattern, topology and branch lengths correspond to the following tree:

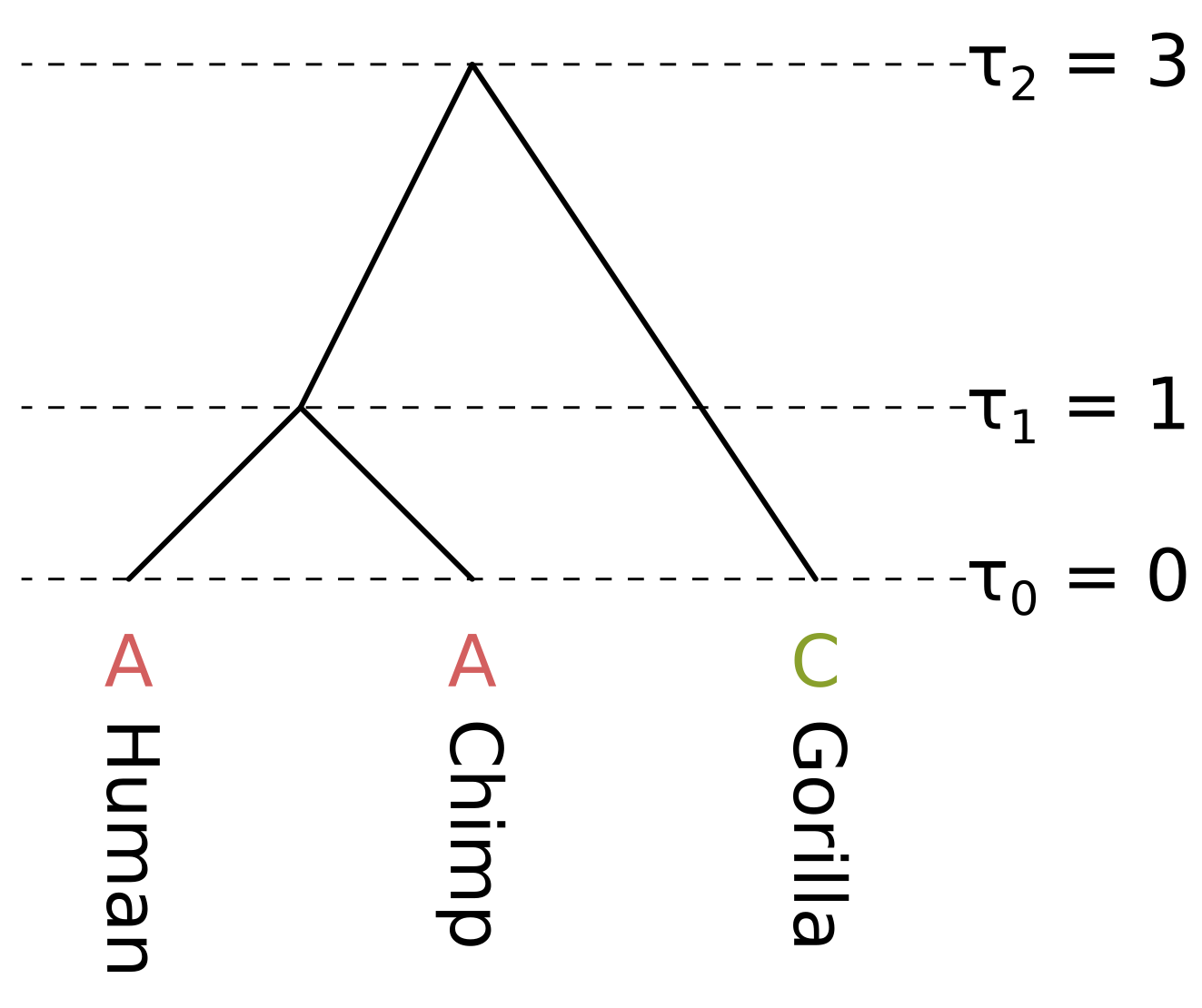
The node heights \(\tau\) are given in some unit of time \(t\) before present. As long as the substitution rate \(\mu\) is constant across the tree (i.e. we are assuming a strict molecular clock), there are three unique branch lengths \(l = \mu t\) in expected substitutions per site. In this example we assume a constant rate \(\mu = 0.1\).

The branch lengths of humans and chimps in substitutions per site are both 0.1, the branch length of the ancestor of humans and chimps (HC) is 0.2, and the branch length of gorillas is 0.3. We will calculate the likelihood under the Jukes–Cantor model, so we only have to calculate the probability of the state being the same by the end of a branch (e.g. A to A), and the probability of the state being something else (e.g. A to C), given the state at the beginning and the branch length.

For the human and chimp branches, these will be (to four decimal places):

\[P_{xx}(0.1) = \frac{1}{4}\left(1 + 3e^{-\frac{4}{3}0.1}\right) = 0.9064\] \[P_{xy}(0.1) = \frac{1}{4}\left(1 - e^{-\frac{4}{3}0.1}\right) = 0.0312\]

For the HC branch, these will be:

\[P_{xx}(0.2) = \frac{1}{4}\left(1 + 3e^{-\frac{4}{3}0.2}\right) = 0.8245\] \[P_{xy}(0.2) = \frac{1}{4}\left(1 - e^{-\frac{4}{3}0.2}\right) = 0.0585\]

For the gorilla branch, these will be:

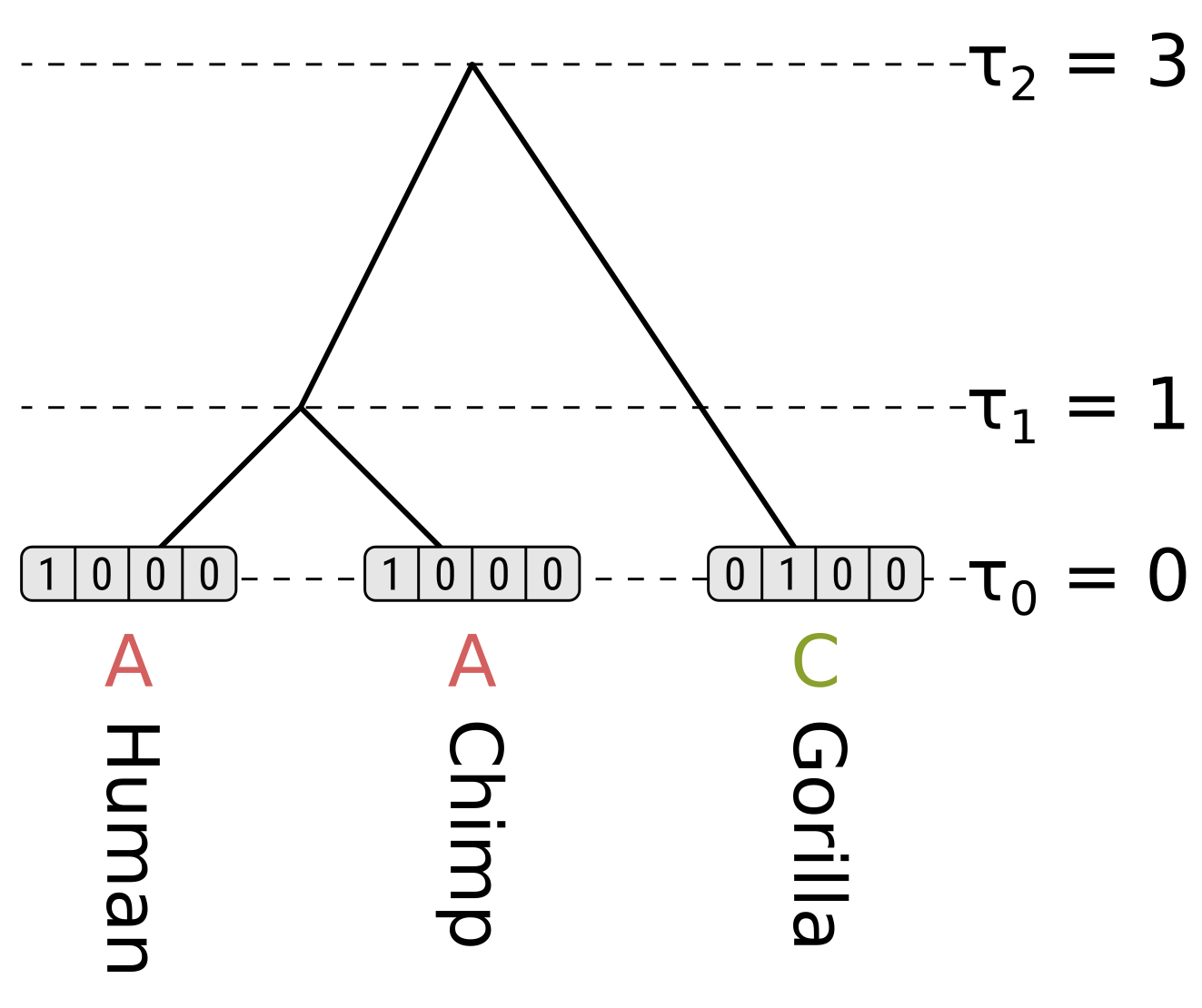
\[P_{xx}(0.3) = \frac{1}{4}\left(1 + 3e^{-\frac{4}{3}0.3}\right) = 0.7528\] \[P_{xy}(0.3) = \frac{1}{4}\left(1 - e^{-\frac{4}{3}0.3}\right) = 0.0824\]

For the tip nodes, the partial likelihoods are 1 for the observed states, and 0 otherwise:

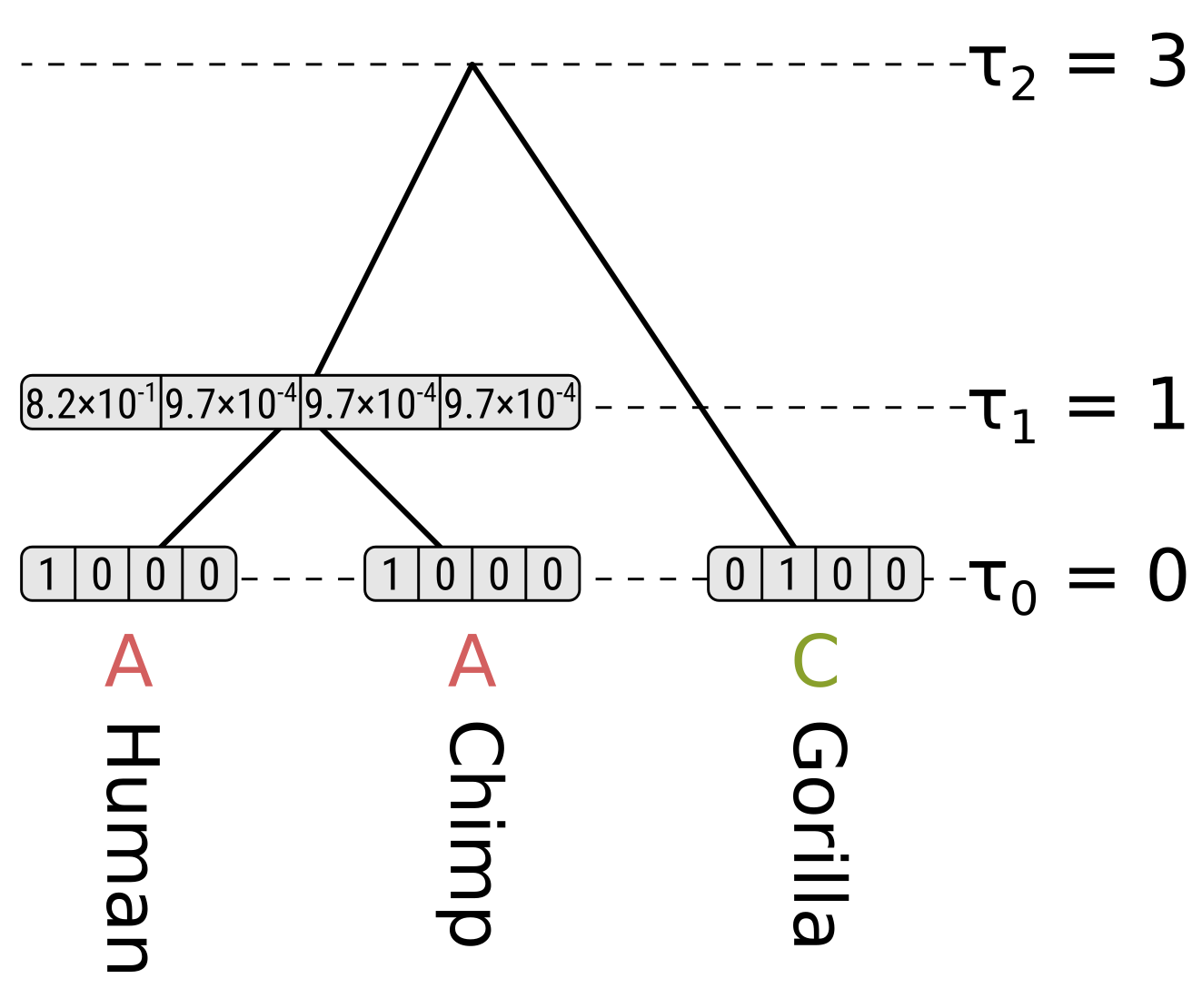
For each internal node we have to consider the left and right children separately. We will start off by calculating the partial likelihood of state A of the HC internal node. Beginning with the left child (humans), the probability of the child state being A is the probability of the end state being the same (as calculated above), multiplied by the partial likelihood of the child state. This is \(0.9064 \times 1 = 0.9064\). For child states C, G and T, the probabilities will be \(0.0312 \times 0 = 0\), so the probability for the left child branch integrating over all child states is \(0.9064 + 0 + 0 + 0 = 0.9064\).

The right child (chimpanzees) has the same branch length and partial likelihoods, so its probability will also be \(0.9064\), and the partial likelihood of state A for the HC node will be \(0.9064 \times 0.9064 = 0.8215\). We use the product because we want to calculate the probability of the left and right subtree states.

For state C in the HC node, the probability along the left branch for child state A will be \(0.0312 \times 1 = 0.0312\). The probability for state C will be \(0.9064 \times 0 = 0\), and for states G and T will be \(0.0312 \times 0 = 0\). So the probability for the left branch integrating over child states will be \(0.0312\). Again the right branch will be the same, so the partial likelihood of state C will be \(0.0312 \times 0.0312 = 0.00097\)

Because of the equal base frequencies and equal rates assumption in Jukes–Cantor, the partial likelihoods of G and T will be the same as for C.

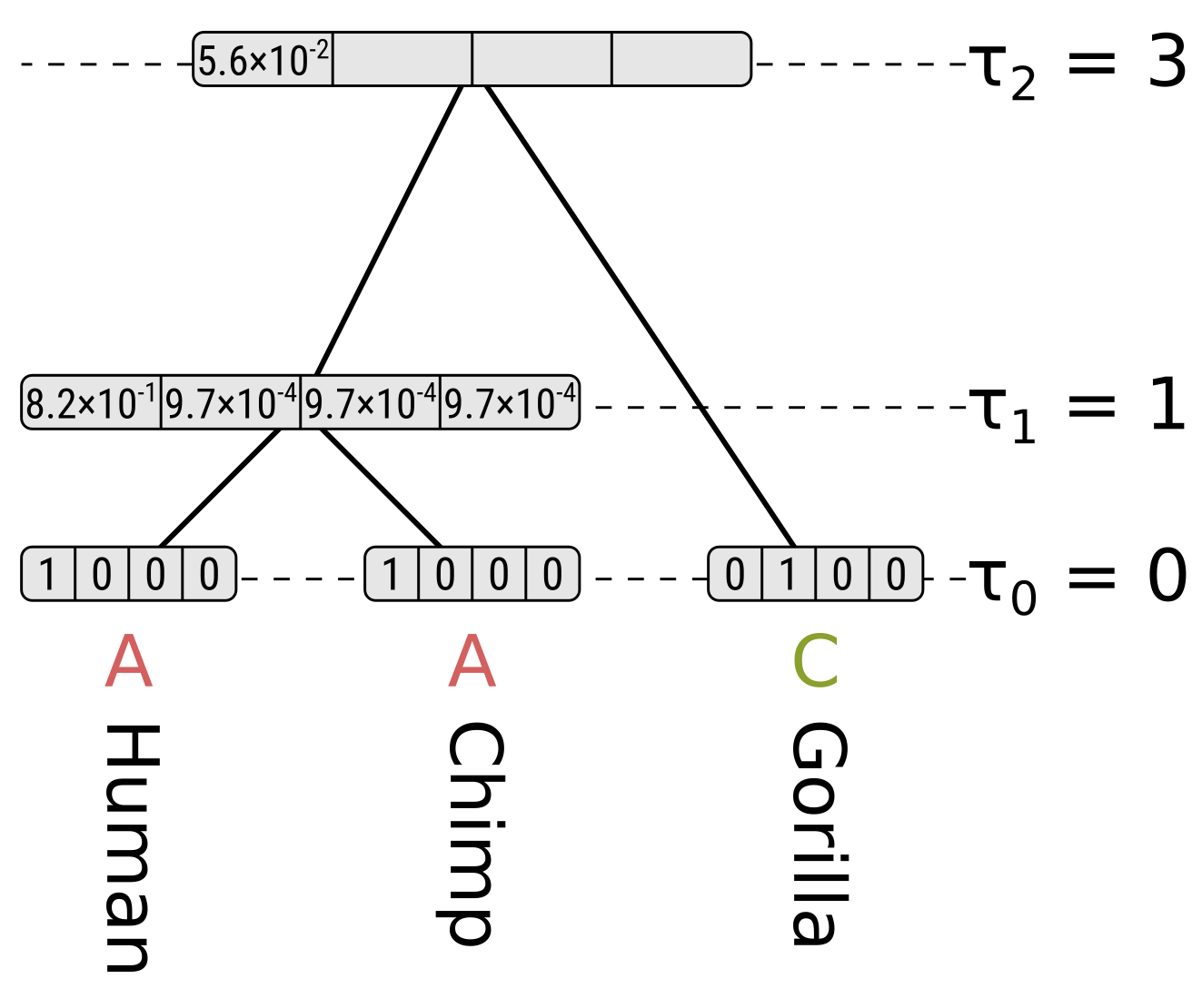
Now for state A at the root, the probability along the left branch for child state A will be the probability of the state remaining the same given a branch length of 0.2, multiplied by the partial likelihood of state A for the HC node, or \(0.8245 \times 0.8215 = 0.6773\). For child states C, G and T it will be \(0.0585 \times 0.00097 = 0.000057\), which is the probability of the state being different at the end given a branch length of 0.2 multiplied by the partial likelihoods. So the probability along the left branch for state A at the root integrating over the left child states will be \(0.6773 + 3 \times 0.000057 = 0.6775\).

For the right child (gorillas) only state C has a non-zero partial likelihood, so we should multiply the above by the probability of a different state given the branch length 0.3 to get the partial likelihood of state A at the root, which will be \(0.6775 \times 0.0824 = 0.0558\).

For state C at the root, the probability of child state A along the left (HC) branch will be \(0.0585 \times 0.8215 = 0.0481\), the probability of child state C will be \(0.8245 \times 0.00097 = 0.0008\), and the probabilities of child states G or T will be \(0.0585 \times 0.00097 = 0.000057\). So integrating over the child states for the left branch, the probability will be \(0.0481 + 0.0008 + 2 \times 0.000057 = 0.0490\). Again because of the symmetry in Jukes–Cantor, the probability along the left branch will be the same for root states G and T.

However for state C at the root, the probability along the right (gorilla) branch will be the probability of the same state at the end given a branch length of 0.3, but for states G and T the probabilities will be for a different state. So for state C at the root the partial likelihood will be \(0.0490 \times 0.7528 = 0.0369\), but for states G and T their partial likelihoods will be \(0.0490 \times 0.0824 = 0.0040\).

Each partial likelihood for a node \(n\) is conditioned on the state \(k\) at that node \(P(D|n=k,T,h)\), but to calculate the likelihood at a node \(P(D|T,h)\) we need to integrate over the probabilities \(P(D,n=k|T,h)\) for each state at that node. Following the chain rule, we can convert the conditional likelihoods to joint probabilities by multipling the partials by the base (stationary) frequencies. For Jukes–Cantor the base frequencies are all equal and hence \(\frac{1}{4}\) given there are 4 nucleotide states.

So we can calculate the likelihood for the entire tree by summing the root partial likelihoods and dividing by 4. For this tree and site, the likelihood \(P(D|T,h) = \frac{0.0588 + 0.0369 + 2 \times 0.0040}{4} = 0.0252\).