Long branch attraction (in the Felsenstein zone)

Long branch attraction is the phenomenon where two branches which are in truth not sisters are inferred to be sister branches when using maximum parsimony inference. This occurs because, unlike likelihood, parsimony does not take into account branch lengths when computing the parsimony score.

Maximum likelihood inference considers all sites when calculating the likelihood, but only so-called “parsimony informative sites” will end up determining the tree inferred using maximum parsimony. These are sites where at least two tips share a state, and at least two other tips share a state which is different from the first state.

Consider the case of humans, chimps, rats and mice. In truth, humans and chimps should be sisters, as should rats and mice. The parsimony informative sites that support the true tree topology will therefore be those where humans and chimps share a state, and rats and mice share a state which is different from the human/chimp state (site patterns on the left in the below figure).

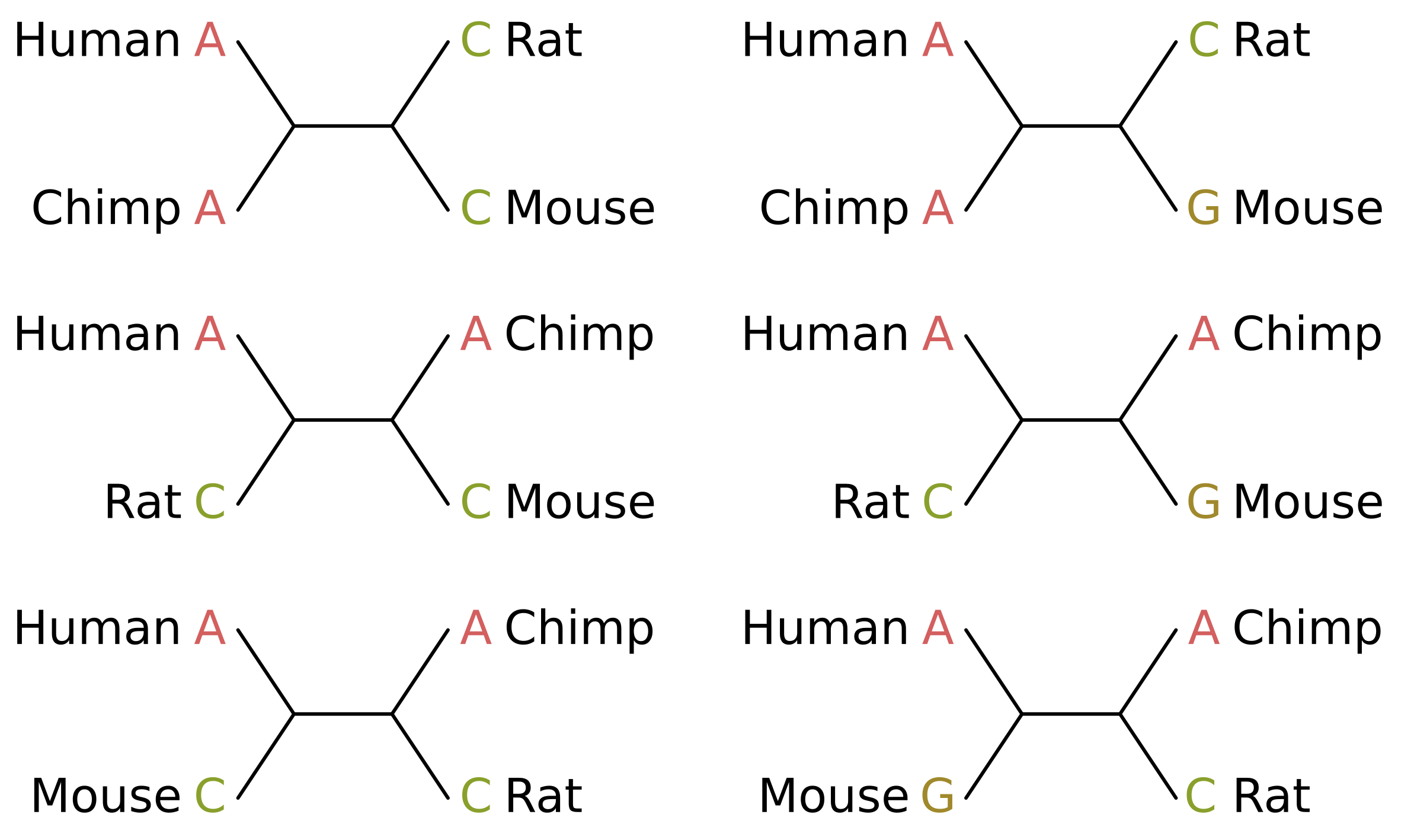
The score of those sites given the true topology (top-left in the above figure) will be 1 for equal-cost parsimony. Given one of the two incorrect unrooted topologies (middle-left and bottom-left), the score of those sites will be 2, because at least two mutations along the tree are required to explain the site pattern.

For the uninformative sites, e.g. if we give mice a different state from every other species (site patterns on the right), at least two mutations will be required for all topologies and the score will always be 2 (see trees on the right). The contribution of these sites is therefore a constant and does not affect the inference.

So if the number of parsimony informative site patterns supporting one of the incorrect topologies is greater than the number of informative site patterns supporting the true topology, the best scoring topology will be incorrect and our inferred topology will be wrong.

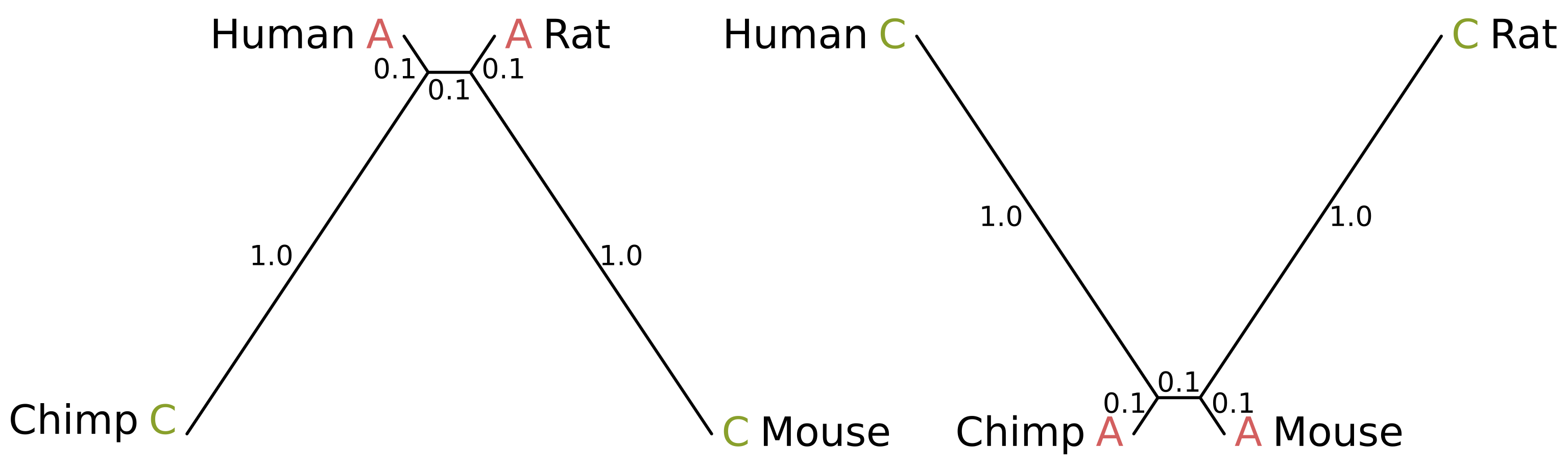
Felsenstein zone trees with branch lengths in substitutions per site

How can this be possible? Consider the above-right tree. Because the internal branch is short, and the chimp and mouse branches are also short, the probability of mutation along those three branches is minimal. Chimps and mice are therefore likely to share a state. But because the human and rat branches are long, the probability of mutation is high.

Given a lack of mutation elsewhere, if a mutation or mutations in the human and rat branches cause the human and rat states to differ, the site will be uninformative. But if convergent mutations occur, the resulting site will be parsimony informative and support the incorrect topology where humans and rats are sister species (for example, the above site patterns).

These sites will contribute a score of 2 to the true topology and a score of 1 to the human-rat topology when using equal-cost parsimony, the inverse of the contribution from parsimony informative sites that support the true human-chimp topology. So if more of the human-rat supporting sites are in a data set than human-chimp supporting sites, the wrong topology will be inferred using maximum parsimony.

How likely is this to occur? I simulated sequence alignments for a range of branch lengths, beginning with the above-left branch lengths, gradually increasing the human and rat lengths (l1) while decreasing the chimp and mouse lengths (l2), ending with the above-right branch lengths. The internal branch length was always 0.1 substitutions per site. Jukes-Cantor was used as the substitution model, 1 million sites were simulated per alignment. For each set of branch lengths I counted the percentage of parsimony informative sites supporting the correct topology and the percentage supporting the human-rat or human-mouse topologies.

You can see that when l1 is greater than somewhere between 0.75 and 0.8 or less than somewhere between 0.3 and 0.35, the number of parsimony informative sites supporting the human-rat topology becomes greater than the number supporting the human-rat topology. These crossovers mark the border of the Felsenstein zone.

For both Dollo and equal rates models of evolution, whether a four-taxon tree is in the Felsenstein zone can be tested analytically rather than by simulation. For details, see Felsenstein’s paper, “Cases in which parsimony or compatibility methods will be positively misleading,” published in Systematic Zoology (now known as Systematic Biology) in 1978.